FINRA Requests Comment on Proposed Changes to TRACE Reporting Relating to Delayed Treasury Spot and Portfolio Trades
FINRA requests comment on two proposed changes to the TRACE reporting rules that were recommended by the Securities and Exchange Commission’s Fixed Income Market Structure Advisory Committee. The proposed changes would require firms to: (1) identify corporate bond trades where the price of the trade is based on a spread to a benchmark Treasury security that was agreed upon earlier in the day (i.e., a “delayed Treasury spot trade”) and report the time at which the spread was agreed upon; and (2) identify corporate bond trades that are a part of a larger portfolio trade.
The proposed rule text is set forth in Attachment A.
Questions regarding this Notice should be directed to:
- Patrick Geraghty, Vice President, Market Regulation, at (240) 386-4973 or by email;
- Elliot Levine, Associate Vice President & Counsel, Transparency Services, at (202) 728-8405 or by email;
- Racquel Russell, Associate General Counsel, Office of General Counsel (OGC), at (202) 728-8363 or by email; or
- Robert McNamee, Assistant General Counsel, OGC, at (202) 728-8012 or by email.
Action Requested
FINRA encourages all interested parties to comment on this proposal. Comments must be received by September 14, 2020.
Comments must be submitted through one of the following methods:
- Emailing comments to [email protected]; or
- Mailing comments in hard copy to:
Jennifer Piorko Mitchell
Office of the Corporate Secretary
FINRA
1735 K Street, NW
Washington, DC 20006-1506
To help FINRA process and review comments more efficiently, persons should use only one method to comment on the proposal.
Important Notes: The only comments that FINRA will consider are those submitted pursuant to the methods described above. All comments received in response to this Notice will be made available to the public on the FINRA website. In general, FINRA will post comments as they are received.1
Before becoming effective, the proposed rule change must be filed with the SEC pursuant to Section 19(b) of the Securities Exchange Act of 1934 (SEA).2
Background and Discussion
On February 10, 2020, the Securities and Exchange Commission’s (SEC) Fixed Income Market Structure Advisory Committee (FIMSAC) unanimously approved a recommendation for FINRA to amend its TRACE reporting rules to provide additional information on two types of trades in corporate bond TRACE-Eligible Securities.3 In these trades, the reported price may not be reflective of the current market for the bond at the time the trades are reported and disseminated. The two types of trades are: (1) delayed Treasury spot trades and (2) portfolio trades.4 The FIMSAC believed that regulatory audit trail data and price transparency could be improved if these trades were specifically identified in TRACE data.5 FINRA is issuing this Regulatory Notice to solicit comment on the usefulness of the changes recommended by the FIMSAC, and on whether any modifications to the scope of the proposal might be appropriate.
A. Delayed Treasury Spot Trades
Market participants may trade corporate bonds on the basis of a spread to a benchmark U.S. Treasury Security,6 which is then converted to a dollar price by “spotting” the benchmark U.S. Treasury Security at a designated time. For example, parties may determine to trade a corporate bond based on an agreed spread to a specified U.S. Treasury Security at 10:00 a.m., but the dollar price is determined later, e.g., at 3:00 p.m., when the parties spot the spread against the benchmark U.S. Treasury Security yield. The TRACE reporting rules generally require firms to report transactions in corporate bonds within 15 minutes of the Time of Execution,7 which is the time when the parties agree to all of the terms of the transaction that are sufficient to calculate the dollar price of the trade.8 Therefore, in the example above, the trade is not reportable to TRACE until the completion of the spotting process (in this example, at 3:00 p.m.), even though the spread and other terms were agreed upon earlier in the day. The FIMSAC believed that a specific modifier for delayed Treasury spot trades, along with disseminating the time at which the spread was agreed, would both alert market participants that the spread-based economics of the trade had been agreed upon earlier in the day as well as provide market participants with the ability to estimate the agreed-upon spread.9
Consistent with the FIMSAC Recommendation, FINRA is proposing two amendments to Rule 6730 to provide additional transparency into delayed Treasury spot trades. Specifically, FINRA is proposing requiring firms to append a new modifier when reporting a transaction in a corporate bond where the price of the transaction is based on a spread to the yield of a U.S. Treasury Security, and where the spread was agreed upon that day prior to the Time of Execution of the transaction. In addition, where the modifier is appended to a delayed Treasury spot trade, firms also would be required to report the time at which the spread was agreed upon (in addition to the Time of Execution).
B. Portfolio Trades
Some market participants also engage in “portfolio trades” in which two parties enter into a single trade for a basket of corporate bonds at an agreed aggregate price for the entire basket. For example, a market participant may seek to trade a portfolio consisting of 50 corporate bonds on an all-or-none or most-or-none basis. The parties may obtain mid-market prices for each of the 50 component bonds as a framework for the pricing, and, during the negotiation process, ultimately agree on a uniform spread, resulting in an aggregate dollar price for the entire portfolio. Even though, in this scenario, the firm is executing a basket of bonds at one, singular price, the TRACE rules require firms to report a trade for each individual bond in the basket with an attributed dollar price for each bond. While, in many cases, the prices attributed to each corporate bond in a portfolio trade may be in line with market levels, in some cases—based on, for example, the liquidity profile of a specific bond or other factors—the attributed price may deviate from the current market price.
The FIMSAC acknowledged that market participants currently may be able to surmise which TRACE reports are part of a portfolio trade (based on a common time of execution or the characteristics of the components). Nonetheless, the FIMSAC believed it would be beneficial if market participants were able to identify with certainty which trades occurred at an agreed price as part of a portfolio trade and, therefore, may not be reflective of the independent market for the bond.10
Consistent with the FIMSAC Recommendation, FINRA is proposing to amend Rule 6730 to require firms to append a new modifier to identify a trade in a corporate bond that has all of the following characteristics: (i) executed between two parties; (ii) involving a basket of corporate bond securities of at least 30 unique issuers; (iii) for a single agreed price for the entire basket; and (iv) executed on an all-or-none or most-or-none basis.
Economic Impact Assessment
Regulatory Objective
As discussed above, prices reported to TRACE for delayed Treasury spot trades and portfolio trades may not be reflective of the current market price for the bonds and may be less informative for market participants that rely on TRACE for price discovery or other analyses. The proposed modifiers would specifically identify these types of trades in disseminated data.
Economic Baseline
A. Delayed Treasury Spot Trades
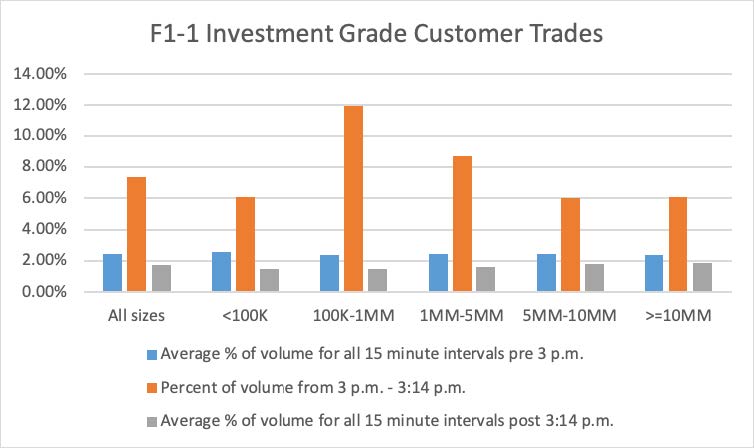
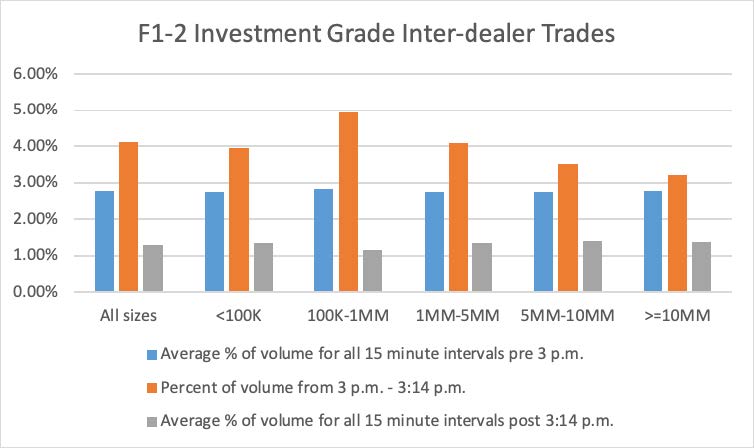
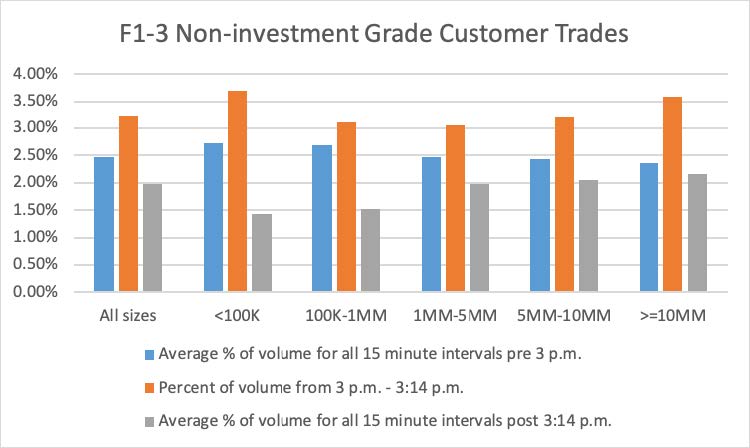
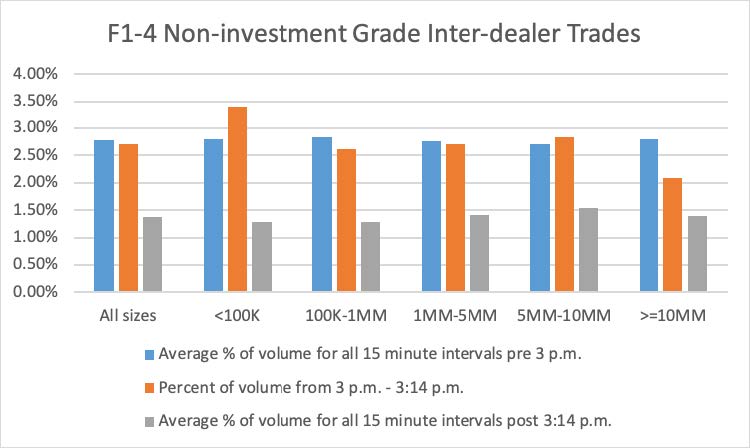
Using 2019 TRACE data, FINRA examined the daily average concentration of corporate bond trades around 3:00 p.m., which is the delayed spot time usually used by dealers. Figures F1-1 and F1-2 below compare, for 2019, the percentage of dollar par volume during the 3:00 p.m. to 3:14 p.m. time interval with: (1) the average percentage of dollar par volume for all 15-minute intervals before 3:00 p.m.; and (2) and the average percentage of dollar par volume for all 15-minute intervals after 3:14 p.m. Figures F1-1 and F1-2 also provide these volume distributions based on the size of trades and for all trades combined. Figure F1-1 provides statistics for customer trades in investment grade bonds and Figure F1-2 provides statistics for inter-dealer trades in investment grade bonds. Figures F1-1 and F1-2 show that, across all trade sizes in investment grade bonds, volumes in the 3:00 p.m. trade interval are larger than both the pre-3:00 p.m. and the post-3:14 p.m. intervals. For investment grade customer trades, the 3:00 p.m. volumes are several times larger than volumes during both the pre-3:00 p.m. and the post-3:14 p.m. intervals. Figures F1-3 and F1-4 provide similar information for trades in non-investment grade bonds. These figures show that the differences in dollar volume across the time intervals are much less material in non-investment grade bond trades. Although trades during the 3:00 p.m. to 3:14 p.m. interval may not all be delayed spot trades, the jump in investment grade bond volume during this period is consistent with FINRA’s understanding of when delayed Treasury spot trades are priced and reported (regardless of when the spread was agreed upon).
Figure 1: Distribution of Corporate Bond Trading Volume during Trading Hours (2019 Daily Average)
B. Portfolio Trades
Evidence supports the hypothesis that portfolio trading has been increasing over time.11 An analysis by Morgan Stanley shows that $88 billion in portfolio trades were executed from January 2019 through November 2019, compared to virtually none in 2017.12 The analysis also shows that portfolio trades with 140 bonds or more increased tenfold since 2018. According to a Financial Times article citing Greenwich Associates’ survey of 67 bond traders, more than 50 percent of the traders executed a portfolio trade in the past year.13
FINRA computed the number and dollar par value of portfolio trades from 2015 to 2019 using TRACE data. For purposes of these calculations, a “portfolio trade” is a trade of a basket of corporate bonds between only two parties at the same execution time.14 Table 1-1 includes portfolio trades by the number of unique CUSIPs identified to be contained in the basket. This analysis demonstrates that portfolio trades reported to TRACE grew significantly in the past five years. For portfolio trades with more than 10 CUSIPs, the total number of portfolio trades approximately tripled from 6,683 in 2015 to 19,001 in 2019. Table 1-2 demonstrates that the total dollar par value grew from approximately $19 million to $340 billion over the past five years. For portfolio trades with at least 30 CUSIPs, the total number of portfolio trades in 2019 was 5,085 (compared to 354 in 2015) and the total dollar par value was approximately $253 billion (compared to $7 billion in 2015). Tables 1-3 and 1-4 show portfolio trades by the number of unique issuers contained in the basket. The results are largely similar.
Table 1-1: Number of Portfolio Trades (Unique CUSIPs)
| By Unique CUSIPs | 2015 | 2016 | 2017 | 2018 | 2019 | 2019 Individual Basket Size Group as % of Total |
|---|---|---|---|---|---|---|
| 1: Customer | 5,775 | 5,815 | 4,778 | 7,225 | 10,116 | 100% |
| 1: >= 10 < 30 | 5,469 | 5,600 | 4,527 | 6,480 | 8,545 | 84.5% |
| 2: >= 30 < 50 | 164 | 188 | 146 | 327 | 695 | 6.9% |
| 3: >= 50 < 70 | 52 | 8 | 33 | 119 | 277 | 2.7% |
| 4: >= 70 < 90 | 22 | 8 | 16 | 53 | 172 | 1.7% |
| 5: >= 90 < 110 | 26 | 2 | 7 | 47 | 103 | 1.0% |
| 6: >= 110 < 130 | 9 | 8 | 23 | 53 | 0.5% | |
| 7: >= 130 | 33 | 9 | 41 | 176 | 271 | 2.7% |
| 2: Dealer to Dealer | 844 | 2,352 | 3,174 | 4,436 | 7,562 | 100% |
| 1: >= 10 < 30 | 836 | 2,229 | 3,009 | 3,358 | 4,804 | 63.5% |
| 2: >= 30 < 50 | 8 | 114 | 147 | 416 | 929 | 12.3% |
| 3: >= 50 < 70 | 0 | 7 | 14 | 173 | 496 | 6.6% |
| 4: >= 70 < 90 | 2 | 0 | 106 | 320 | 4.2% | |
| 5: >= 90 < 110 | 0 | 78 | 245 | 3.2% | ||
| 6: >= 110 < 130 | 0 | 48 | 197 | 2.6% | ||
| 7: >= 130 | 4 | 257 | 571 | 7.6% | ||
| 3: Non-Member Affiliate | 64 | 455 | 259 | 2,524 | 1,323 | 100% |
| 1: >= 10 < 30 | 24 | 179 | 129 | 2,136 | 567 | 42.9% |
| 2: >= 30 < 50 | 12 | 73 | 55 | 126 | 194 | 14.7% |
| 3: >= 50 < 70 | 17 | 60 | 32 | 56 | 102 | 7.7% |
| 4: >= 70 < 90 | 4 | 49 | 14 | 58 | 103 | 7.8% |
| 5: >= 90 < 110 | 2 | 38 | 13 | 29 | 57 | 4.3% |
| 6: >= 110 < 130 | 2 | 15 | 5 | 26 | 28 | 2.1% |
| 7: >= 130 | 3 | 41 | 11 | 93 | 272 | 20.6% |
| Grand Total | 6,683 | 8,622 | 8,211 | 14,185 | 19,001 | |
| Total >=30 | 354 | 614 | 546 | 2,211 | 5,085 | |
| % of >=30 as Grand Total | 5.3% | 7.1% | 6.6% | 15.6% | 26.8% |
Table 1-2: Dollar Par Value (Million, Unique CUSIPs)
| By Unique CUSIPs | 2015 | 2016 | 2017 | 2018 | 2019 | 2019 Individual Basket Size Group as % of Total |
|---|---|---|---|---|---|---|
| 1: >= 10 < 30 | 11,458 | 17,734 | 18,474 | 42,984 | 86,937 | 25.6% |
| 2: >= 30 < 50 | 1,254 | 2,243 | 2,119 | 17,298 | 43,779 | 12.9% |
| 3: >= 50 < 70 | 1,289 | 1,718 | 2,980 | 9,992 | 35,621 | 10.5% |
| 4: >= 70 < 90 | 788 | 1,735 | 828 | 6,463 | 30,916 | 9.1% |
| 5: >= 90 < 110 | 1,269 | 1,169 | 2,024 | 6,186 | 18,623 | 5.5% |
| 6: >= 110 < 130 | 507 | 587 | 335 | 3,272 | 18,277 | 5.4% |
| 7: >= 130 | 1,950 | 3,065 | 2,983 | 54,581 | 105,674 | 31.1% |
| Grand Total | 18,515 | 28,251 | 29,745 | 140,776 | 339,826 | 100% |
| Total >=30 | 7,056 | 10,517 | 11,270 | 97,792 | 252,890 | |
| % of >=30 as Grand Total | 38.1% | 37.2% | 37.9% | 69.5% | 74.4% |
Table 1-3: Number of Portfolio Trades (Unique Issuers)
| By Unique Issuers | 2015 | 2016 | 2017 | 2018 | 2019 | 2019 Individual Basket Size Group as % of Total |
|---|---|---|---|---|---|---|
| 1: Customer | 4,633 | 4,779 | 4,119 | 6,150 | 8,829 | 100% |
| 1: >= 10 < 30 | 4,385 | 4,686 | 3,940 | 5,531 | 7,543 | 85.4% |
| 2: >= 30 < 50 | 134 | 73 | 100 | 259 | 589 | 6.7% |
| 3: >= 50 < 70 | 39 | 9 | 23 | 110 | 268 | 3.0% |
| 4: >= 70 < 90 | 29 | 3 | 11 | 61 | 128 | 1.4% |
| 5: >= 90 < 110 | 18 | 12 | 42 | 76 | 0.9% | |
| 6: >= 110 < 130 | 10 | 1 | 13 | 29 | 61 | 0.7% |
| 7: >= 130 | 18 | 7 | 20 | 118 | 164 | 1.9% |
| 2: Dealer to Dealer | 709 | 1,937 | 2,652 | 3,878 | 6,885 | 100% |
| 1: >= 10 < 30 | 707 | 1,871 | 2,572 | 2,986 | 4,420 | 64.2% |
| 2: >= 30 < 50 | 2 | 66 | 72 | 342 | 933 | 13.6% |
| 3: >= 50 < 70 | 0 | 0 | 6 | 167 | 475 | 6.9% |
| 4: >= 70 < 90 | 103 | 360 | 5.2% | |||
| 5: >= 90 < 110 | 0 | 76 | 263 | 3.8% | ||
| 6: >= 110 < 130 | 0 | 68 | 168 | 2.4% | ||
| 7: >= 130 | 2 | 136 | 266 | 3.9% | ||
| 3: Non-Member Affiliate | 60 | 418 | 226 | 1,995 | 1,189 | 100% |
| 1: >= 10 < 30 | 26 | 169 | 118 | 1,714 | 608 | 51.1% |
| 2: >= 30 < 50 | 16 | 78 | 60 | 116 | 182 | 15.3% |
| 3: >= 50 < 70 | 10 | 74 | 20 | 58 | 81 | 6.8% |
| 4: >= 70 < 90 | 3 | 46 | 15 | 51 | 70 | 5.9% |
| 5: >= 90 < 110 | 2 | 17 | 5 | 28 | 45 | 3.8% |
| 6: >= 110 < 130 | 1 | 12 | 3 | 7 | 50 | 4.2% |
| 7: >= 130 | 2 | 22 | 5 | 21 | 153 | 12.9% |
| Grand Total | 5,402 | 7,134 | 6,997 | 12,023 | 16,903 |
|
| Total >=30 | 284 | 408 | 367 | 1,792 | 4,332 |
|
| % of >=30 as Grand Total | 5.3% | 5.7% | 5.2% | 14.9% | 25.6% |
|
Table 1-4: Dollar Par Value (Million, Unique Issuers)
| By Unique Issuers | 2015 | 2016 | 2017 | 2018 | 2019 | 2019 Individual Basket Size Group as % of Total |
|---|---|---|---|---|---|---|
|
1: >= 10 < 30 |
9,302 | 14,387 | 15,697 | 42,728 | 92,864 | 28.4% |
|
2: >= 30 < 50 |
1,627 | 2,503 | 3,384 | 17,508 | 55,327 | 16.9% |
|
3: >= 50 < 70 |
1,207 | 2,325 | 930 | 10,666 | 38,486 | 11.8% |
|
4: >= 70 < 90 |
1,461 | 1,605 | 2,172 | 9,368 | 28,869 | 8.8% |
|
5: >= 90 < 110 |
689 | 758 | 1,073 | 11,286 | 20,819 | 6.4% |
|
6: >= 110 < 130 |
538 | 620 | 800 | 6,440 | 17,297 | 5.3% |
|
7: >= 130 |
1,228 | 1,976 | 1,322 | 35,560 | 73,371 | 22.4% |
|
Grand Total |
16,051 | 24,173 | 25,379 | 133,555 | 327,034 | 100% |
|
Total >=30 |
6,749 | 9,786 | 9,681 | 90,827 | 234,169 |
|
|
% of >=30 as Grand Total |
42.0% | 40.5% | 38.1% | 68.0% | 71.6% |
|
Economic Impact
-
Delayed Treasury Spot Trades
A modifier identifying delayed Treasury spot trades may add valuable information to disseminated TRACE data by indicating that the reported price may not be at the current market. The new disseminated field providing the time at which the spread was agreed upon could benefit the market by providing participants with this information, which market participants may use to reasonably evaluate the transaction price compared to other prices reported to TRACE at or near the same time. Below, FINRA requests comment on whether this proposal would provide useful information to the marketplace.
FINRA and members would be required to make systems changes to accommodate the new modifier and time field. This would represent a fixed cost to FINRA and its members that report corporate bond transactions priced through a delayed Treasury spot process. The variable cost of reporting the new modifier and populating the time field should be minimal for firms as costs currently are incurred for existing TRACE reporting. We request comment below on the costs associated with the proposed changes.
-
Portfolio Trades
A modifier identifying trades executed as part of a portfolio trade would allow market participants to identify with certainty which trades occurred at attributed prices as part of a portfolio trade. With this information, market participants could better identify trade prices that may not reflect the market price if the bond was priced individually. Below, FINRA requests comment on whether this proposal would provide useful information to the marketplace.
FINRA and members would incur costs associated with making system changes required to accommodate the new modifier. This would represent a fixed cost to FINRA and its members that execute and report portfolio trades. The variable cost of reporting the new modifier should be minimal to firms as costs are currently incurred for existing TRACE reporting. In addition, while market participants currently may infer that some trades may be portfolio trades, they cannot do so with certainty. The FIMSAC noted that there may be an increased theoretical risk that a market participant may identify the seller of a portfolio trade if these trades are identified in disseminated data.15 It is difficult for FINRA to analyze the extent of the risk given the inability to ascertain the extent to which market participants can identify trades that are part of a portfolio with existing data. FINRA requests comment below on the costs associated with the proposed changes.
Alternatives Considered
No alternatives have been considered.
Request for Comment
FINRA requests comment on all aspects of the proposal. FINRA requests that commenters provide empirical data or other factual support for their comments wherever possible. In addition to general comments, FINRA specifically requests comments on the following questions.
Delayed Treasury Spot Trades
As discussed above, FINRA is proposing to amend Rule 6730 to require firms to append a new modifier to identify a corporate bond transaction that was priced earlier in the day based on the spread to a U.S. Treasury Security. Under the proposal, firms also would report the time at which the parties agreed to the spread.
- FINRA requests comment on whether the proposed new modifier and time field would provide useful information to the marketplace. Why or why not?
- If the new modifier and time field provide benefits, will they benefit some market participants more than others? If so, why?
- Are there any modifications or alternatives to the current proposal that FINRA should consider in providing additional insight into delayed Treasury spot trades?
- For example, should FINRA consider requiring firms to report the spread, either at the time that the spread is agreed upon or later in the day when the dollar price is known?
- If the spread should be reported, should this information be reported in lieu of or in addition to the time at which the spread was agreed upon?
- If the spread should be reported at the time it is agreed upon, should the dollar price also be reported later in the day when known?
- Once the spread and benchmark are agreed upon, are there circumstances under which they may change before the trade is finalized?
- Should FINRA consider requiring firms to identify the benchmark U.S. Treasury Security being used to price a delayed Treasury spot trade so that market participants can calculate the spread with certainty? Why or why not?
- What operational or other challenges would be associated with these alternatives?
- FINRA understands that the most common pricing benchmark used for delayed Treasury spot trades is the on-the-run U.S. Treasury Security with the maturity that corresponds to the maturity of the corporate bond being priced (g., the most recently issued 10-year U.S. Treasury Security typically is used as the benchmark for pricing a 10-year corporate bond issue). FINRA requests comment on whether this understanding is accurate. To the extent that market participants would not use the most recently issued U.S. Treasury Security with the same maturity, please discuss alternative ways in which a U.S. Treasury benchmark may be chosen and provide insight into the frequency of use of these alternatives.
- Do commenters anticipate any challenges with identifying delayed Treasury spot trades or with reporting the time at which the spread was agreed in a timely manner?
- What costs are associated with identifying delayed Treasury spot trades or the time at which the spread was agreed upon?
- Will the new requirements impose costs on some reporters more than others? If so, why?
- What operational or other challenges would be associated with implementing the proposal?
- What costs are associated with modifying firms’ reporting systems to append the new modifier and populate the new time field?
- How much time would firms need to make systems and other changes required to implement the proposal?
- Will there be any other costs for TRACE reporters or other market participants related to the proposal? If so, please describe.
Portfolio Trades
As discussed above, FINRA is proposing to amend Rule 6730 to require firms to append a new modifier to identify a trade in a corporate bond (i) executed between two parties; (ii) involving a basket of corporate bond securities of at least 30 unique issuers; (iii) for a single agreed price for the entire basket; and (iv) executed on an all-or-none or most-or-none basis.
- FINRA requests comment on whether the proposed new modifier would provide useful information to the marketplace. Why or why not?
- If the new modifier provides benefits, will it benefit some market participants more than others? If so, why?
- FINRA also requests comment on whether the proposed parameters are appropriate.
- For example, is “at least 30 unique issuers” the appropriate threshold for appending the new modifier, or would a different threshold be more appropriate? If a different threshold would be more appropriate, please specify.
- Should the proposed portfolio trade modifier be appended to trades involving at least 30 unique CUSIPs, rather unique issuers (as is currently proposed)? Why or why not?
- What operational or other challenges would be associated with these alternative parameters?
- Are there any other modifications or alternatives that FINRA should consider in providing additional insight into portfolio trades? If so, please explain.
- FINRA requests comment on firms’ current practices for attributing a price to each component of a portfolio trade for purposes of reporting the individual bond transaction to TRACE. What methodologies and associated documentation do firms have in place and keep regarding attributing a price to component securities for portfolio trades?
- FINRA requests comment on the probability that a market participant would be able to identify the counterparties to a portfolio trade if such trades are identified in disseminated data. How would this probability compare to the probability that counterparties could be identified based on current TRACE data? What effect might this have on the market?
- What costs are associated with identifying portfolio trades?
- Will the new requirements impose costs on some reporters more than others? If so, why?
- What operational or other challenges would be associated with implementing the proposal?
- What costs are associated with modifying firms’ reporting systems to append the new portfolio trade modifier?
- How much time would firms need to make systems and other changes to implement the proposal?
Will there be any other costs for TRACE reporters or other market participants? If so, please describe.
Endnotes
- FINRA will not edit personal identifying information, such as names or email addresses, from submissions. Persons should submit only information that they wish to make publicly available. See Notice to Members 03-73 (November 2003) (Online Availability of Comments) for more information.
- See SEA Section 19 and rules thereunder. After a proposed rule change is filed with the SEC, the proposed rule change generally is published for public comment in the Federal Register. Some proposed rule changes take effect immediately upon filing with the SEC. See SEA Section 19(b)(3) and SEA Rule 19b-4.
- Rule 6710(a) generally defines a “TRACE-Eligible Security” as a debt security that is United States (“U.S.”) dollar-denominated and is: (1) issued by a U.S. or foreign private issuer, and, if a “restricted security” as defined in Securities Act Rule 144(a)(3), sold pursuant to Securities Act Rule 144A; (2) issued or guaranteed by an Agency as defined in Rule 6710(k) or a Government-Sponsored Enterprise as defined in Rule 6710(n); or (3) a U.S. Treasury Security as defined in Rule 6710(p). “TRACE-Eligible Security” does not include a debt security that is issued by a foreign sovereign or a Money Market Instrument as defined in Rule 6710(o).
- See Recommendation Regarding Additional TRACE Reporting Indicators for Corporate Bond Trades (February 10, 2020), (“FIMSAC Recommendation”). The FIMSAC recommended that these proposals apply only to corporate bond transactions reported to TRACE.
- FINRA reminds members that, pursuant to Rule 3110 (Supervision), they must have policies and procedures in place that are reasonably designed to ensure compliance with the 6700 Rule Series (Trade Reporting and Compliance Engine (TRACE)), including the accurate reporting of applicable trade modifiers or indicators. Firms also must be able to demonstrate that a transaction meets the applicable conditions associated with a particular modifier or indicator.
- Rule 6710 defines a “U.S. Treasury Security” as “a security, other than a savings bond, issued by the U.S. Department of the Treasury to fund the operations of the federal government or to retire such outstanding securities.” The term “U.S. Treasury Security” also includes separate principal and interest components of a U.S. Treasury Security that has been separated pursuant to the Separate Trading of Registered Interest and Principal of Securities (“STRIPS”) program operated by the U.S. Department of Treasury. See Rule 6710(p).
- See Rule 6730(a).
- See Rule 6710(d).
- See FIMSAC Recommendation at 2.
- See id.
- See infra notes 12 and 13.
- See Jennifer Surane and Matthew Leising, “Bond Trade That’s Gone from Zero to $88 Billion in Two Years,” Bloomberg (Nov. 18, 2019).
- See Joe Rennison, Robert Armstrong and Robin Wigglesworth, “The New Kings of the Bond Market,” Financial Times (Jan. 22, 2020). Among those traders, 75 percent executed the portfolio trade with dealers while the remaining did so through other means, such as an electronic trading platform.
- Using only current TRACE data, FINRA cannot identify “portfolio trades,” as defined in the FIMSAC Recommendation. Specifically, the analysis in this Notice may include trades that are not executed at a single agreed price for the entire basket and that are not executed on an all-or-none or most-or-none basis. As a result, the method used in this Notice may include as a “portfolio trade” some trades that would fall outside of the scope using the FIMSAC’s criteria. However, FINRA believes that the method used in these calculations is reasonable given the scope of information currently available in TRACE.
- See FIMSAC Recommendation at 2.
| Date | Commenter |
|---|---|
| Melinda Ramirez Comment On Regulatory Notice 20-24 | |
| Financial Information Forum on Reg Notice 20-24 | |
| Bloomberg, L.P. on Reg Notice 20-24 | |
| Jane Street on Reg Notice 20-24 | |
| FIX Trading Community on Reg Notice 20-24 | |
| T.RowePrice on Reg Notice 20-24 | |
| SIFMA on Reg Notice 20-24 |
